-
在线客服
QQ扫码联系在线客服
QQ: 2292620539
-
本文是本系列的第四篇,由于侧重点是对密码学中的安全性问题进行分析,所以不会对密码学基础的核心概念进行阐述,如果阅读本系列文章时不明白所涉及的术语时请参考国内大学的推荐教材,如《密码学原理与实践》《深入浅出密码学》,如果只是感兴趣而并非要深入了解,只阅读《图解密码技术》也就够了。
迪菲-赫尔曼密钥交换/协商(英语:Diffie–Hellman key exchange,缩写为D-H) 是一种安全协议。它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。
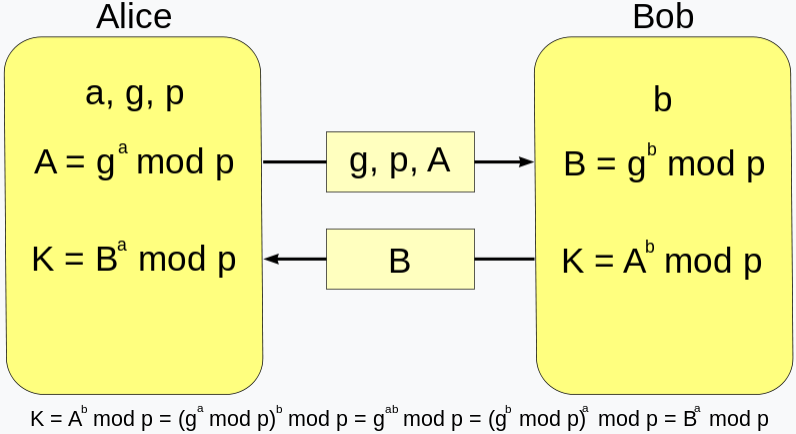
DH密钥协商协议的核心操作是DH函数,其涉及通信双方从Zp*群中随机选择两个私有值,记做a、b,通过a计算公共值A= g^a mod p,通过b计算
B= g^b mod p
然后双方将公共值与自己的私有值结合,这里的关键在于结合后的值是相同的,即
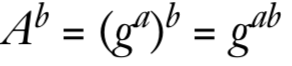
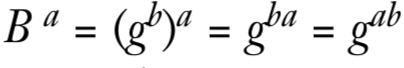
得到的g^ab称为共享秘密,将其传递给密钥派生函数KDF,以生成对称密钥。
这看起来非常简单,但是这只是表面的,事实上这并不容易
一方面,并不是任意素数p或者基数g都可以奏效,比如某些g会导致将共享秘密g^ab限制在一小部分范围内,但实际上我们希望它的可能取值范围与Zp*一样。
p应该满足(p-1)/2结果也是素数,这样才可以保证该群没有使DH更容易被攻破的更小子群。
使用DH计算共享秘密时,我们关心的不仅是DLP问题,更关注特定于DH的问题,分别是CDH和DDH。
CDH即computational Diffie-Hellman,计算DH问题,给定g^a和
g^b,但是不知道a或b时,
求出g^ab
这个问题的出发点是为了确保攻击者即使拿到了双方的公共值,也不知道共享秘密。
如果可以解决DLP,自然可以解决CDH;但是解决CDH,不一定能解决DLP,事实上可以解决CDH的最快方法是用NFS(numer field sieve,数域筛选法)求解DLP
DDH即decisional Diffie-Hellman,这个难度假设比CDH更强,如假设在给定公共值的2048比特情况下,攻击者可以计算共享秘密的前32比特,但是无法计算所有2048比特。此时虽然攻击者不知道完整的g^ab,但是它还是知道共享秘密的一部分信息,这有助于攻击者造成破坏。
为了确保攻击者无法得到关于
g^ab的任何信息,只需要将其与随机的群元素区分开即可,这种问题就称之为DDH。给定公共值和某个随机数c,在公共值和g中二选一(概率均为1/2),
DDH问题确定g^ab是否被选中。
如果DDH很难,那么CDH也会很难,就无法获得g^ab的任何信息;如果可以解决CDH,那么就可以解决DDH.DDH不如CDH难,但是DDH是密码学中的主要假设,也是被研究最多的一种。
通信双方在完成DH会话交换时,会得到共享秘密g^ab,但是,我们要注意,这是作为派生会话密钥的输入,其本身并不是密钥!
我们知道密钥看起来应该是随机的,其本身每个比特为0、1的概率是相同的,但是g^ab做不到这一点,因为它不是随机字符串。这里容易混淆的一点是:随机的群元素与随机的比特字符串本质上是不一样的。
举个例子,设乘法群Z13*={1,2...12},使用g=2作为生成元,根据g^i可以扩展成所有
Z13*的值,如果g的指数是随机的,那么会获得
Z13*的随机元素,但是将对应元素编码为4比特字符串时就不是随机的了
此时的随机的概念要求所有比特位为0或1的概率相同
但是在Z13*中,有7个值的最高比特位为0,只有5个值的最高比特位为1,所以这个比特位为0的概率为7/12,约为0.58,而不是0.5.
CVE-2016-0701是OpenSSL的一个漏洞,其利用的就是不安全的D-H参数,当用户使用不安全的DH群参数(即不安全的素数p)时,会引发风险。
给定素数p,所有DH操作都在其对应的乘法群Zp中发生,Zp包括小的子群.问题在于,在加密协议中如果较大的群中存在较小的子群是非常危险的,因为此时会将共享秘密限制在较小的可能值集合内。更进一步地,攻击者可以构造DH指数x,当其与受害者的公钥g^y结合时,会暴露有关私钥y的信息,从而可能让其完全泄露。
椭圆曲线的安全性在于它使用的群的阶(即曲线的点数),加法公式以及其参数的选取原因。
椭圆曲线有很多,但不是所有的都适用于加密,在选择时要仔细选择曲线方程y^2=
x^3+ax+b中的系数a和b,否则得到的曲线可能是不安全的,一般而言,有如下要求:
1.群的阶不能等于一些小数的乘积,否则会很容易求解ECDLP
2.由于当Q=P时,加法公式与其他情况不同,所以做加法时需要权衡,当攻击者可以区分相同点之间的加法和不同点之间的加法时,可能会泄露关键信息。如果曲线对所有点的加法都使用同一个公式,那么它可能是安全的
3.如果曲线的设计者不解释选择参数a,b的原因,那么曲线可能是不安全的,因为我们并不知道a,b是否是较弱的参数。
常用的曲线有NIST曲线以及Curve25519
NIST的5条曲线工作在模素数上,称为素数曲线,这是最常见的,其中最常用的是P-256,这是对256比特数
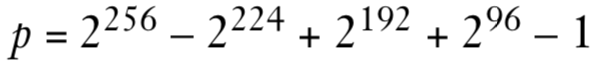
进行模运算的曲线,其对应的方程为
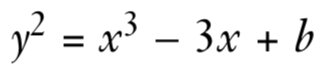
但是NIST曲线的系数选择是由NSA指定的,他们并没有说选b的理由,所以这可能是不安全的。
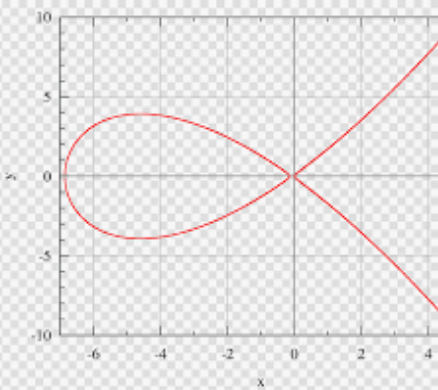
这是由Daniel J.Bernestein设计的,是目前最高水平的 Diffie-Hellman函数,适用于广泛的场景。Curve25519是一个椭圆曲线提供128位安全性,设计用于椭圆曲线Diffie-Hellman(ECDH)密钥协商方案。它是最快的ECC曲线之一。给定一个用户的32字节密钥,curve25519计算该用户的32字节公钥。给定该用户的32字节密钥和另一个用户的32字节公钥,curve25519计算一个32字节的共享密钥提供给这两个用户使用。然后可以使用这个秘密对两个用户进行身份验证和信息加密。其方程形式为
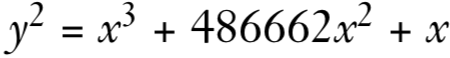
其中486662是满足作者设定的安全准则的最小整数。
其应用十分广泛,包括Chrome,OpenSSH等。
与传统的Diffie-Hellman比起来,椭圆曲线使用的参数更多,更容易受到参数误用的风险,也就更容易受到攻击。
我们知道在ECDSA的签名过程中求s=(h+rd)/k mod n时,使用的k是秘密随机的,所以由此产生的签名也是随机的。
如果相同的k被重用去对第二个消息进行签名,那么攻击者可以通过生成的两个值s1=(h1+rd)/k,s2=(h2+rd)/k,得到s1-s2=(h1-h2)/k,从而有k=(h1-h2)/(s1-s2),当k已知时,通过下式可以恢复私钥d
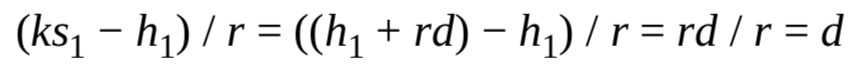
根据椭圆曲线的特点,如果无法验证输入点,那么ECDH就无法正常工作,因为给出点P+Q的坐标的加法公式中没有涉及曲线的系数b,加法公式只依赖于点P和点Q的坐标和系数a,这会导致什么问题呢?
对两个点做加法时,可能其中一个点不在正确的曲线上,即可能加的是另一个只有系数b不同的曲线上的点,这样的话,加法不是在曲线上进行的,攻击者由此就可以发动攻击。
举个例子,设Alice和Bob正在进行ECDH,并在曲线和基点G上达成一致。Bob将其公钥dBG发送给Alice,但是Alice不在约定的曲线上发送自己的公钥dAG,而是发送了另一条曲线上的一个点(而这条曲线非常如,并且对于Alice选择的点P,求解ECDLP很容易,换句话说,Alice选择了一个阶数很低的点,其有一个较小的k,是的kP=O)。而Bob并不知情,通过该公钥计算共享秘密dBP,对他进行哈希,并使用得到的密钥进行加密,并将其发送给Alice。但是,Bob在计算dBP时,不知不觉中计算了较弱的曲线,由于P的阶较低,于是P点落在原本选择的高阶的群的一个小的子群中,导致dBP也在这个小子群中,从而让攻击者在知道P的阶数的情况下有效地确定共享秘密dBP。
一个典型的例子是CVE-2019-9836,研究人员发现SEV椭圆曲线(ECC)实现容易受到无效曲线攻击。在启动命令中,攻击者可以发送不在官方NIST曲线上的小顺序ECC点,并迫使SEV固件将小顺序点乘以固件的专用DH标量。另外这篇学术论文也可供参考《Practical Invalid Curve Attacks on TLS-ECDH》
当一个问题用量子计算机比用经典计算机能更快求解时 ,就称之为量子加速。比如在经典计算机中,要在无序列表中找到某个索引,平均需要n/2次操作。但是存在一种量子算法,只需要√n次操作即可,这比n/2小了几个数量级,比如n=1000000,那么n/2=500000,√n=1000。
我们一般使用时间复杂度来量化算法之间的差异,其用O()符号表示,以上面这个例子为例,经典算法的量级为O(n),而量子算法的运行时间在O(√n)量级,它们之间的差异是平方指数,我们称之为二次加速。
事实上,量级计算还可以实现指数加速,即一个任务在经典计算机上需要指数级时间,如O(2^n),而在量子计算机上只需要多项式复杂度即可,即O(n^k)。因为在密码学中,我们通常把指数时间与不可能联系起来,而多项式时间意味着可实现,所以指数加速对密码学带来的冲击是非常大的。
指数加速的典型代表就是Simon问题:
给定一个方程:

如果使用经典计算机,求解该问题本质可以归结为寻找碰撞,需要求f进行2^(n/2)次查询
而如果使用量子计算机,通过n次查询即可,对应的量子算法电路如下
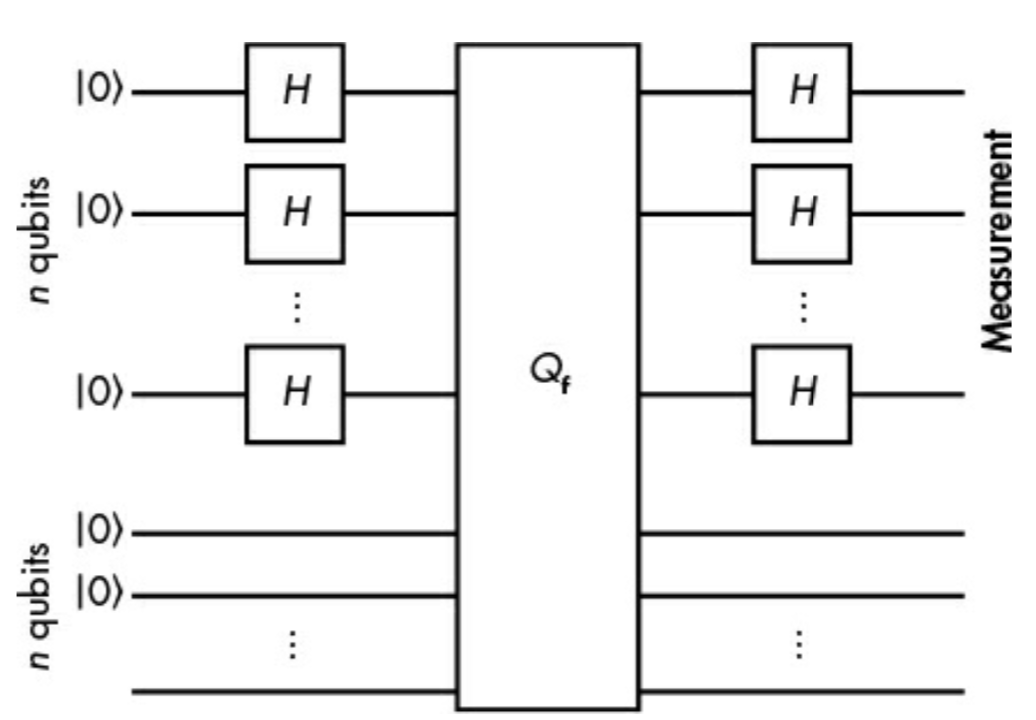
实际上,Simon问题的指数加速只有在非常特定的情况下才能应用于对称密码。我们再来看看更实际的情况
Shor算法作为一种量子算法,可以在求解因式分解、离散对手、椭圆曲线离散对数等问题时实现指数加速,这意味着RSA,D-H、椭圆曲线密码等机制都会受到影响。Shor算法中的量子部分如下图所示
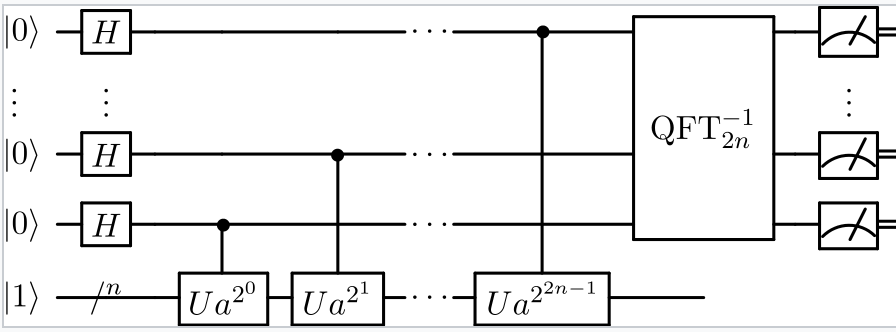
Shor算法实际上解决的问题比因式分解等问题更普遍:如果f是周期函数,即存在f(x+a)=f(x),其中a是周期,则Shor算法可以有效找到周期a。这种高效找到周期的能力对于密码学而言非常重要,可以用其攻击公钥密码。我们来看看Shor怎么解决因式分解和离散对数问题,它们分别对应着RSA和Diffie-Hellman背后的数学难题
设要分解大数N=pq
如果可以计算出a^x mod N的周期就能很容易对N进行因式分解:
选择一个小于N的随机数a,然后向Shor算法询问函数f(x)=a^x mod N的周期,如果找到周期,那么就有
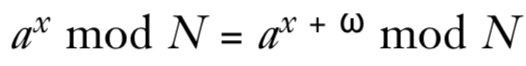
即
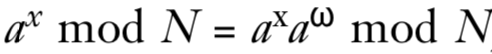
这意味着,要么
![]()
或者
![]()
换句话说,a^ω -1是N的倍数,即存在某个数k,使得下式成立
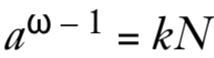
这里的关键在于a^(ω-1)可以很容易分解为两项的乘积
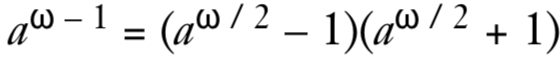
那么就可以计算出a^ω/2 -1与N的最大公约数,并检查是否已经得到N的一个非平凡因数,如果不是,则对另一个值a^ω/2+1做相同运算,尝试几次后,就可以得到N的因数,此时就可以从RSA的公钥中恢复私钥,拿到私钥后就可以解密消息、伪造签名了。
我们来分析下复杂度。对N进行因式分解的经典算法的时间复杂度是n的指数级别,n是N的比特长;而Shor算法在n的多项式时间O(n^2(log n)(log log n))内即可完成。下图是经典大数分解和Shor算法的复杂度对比
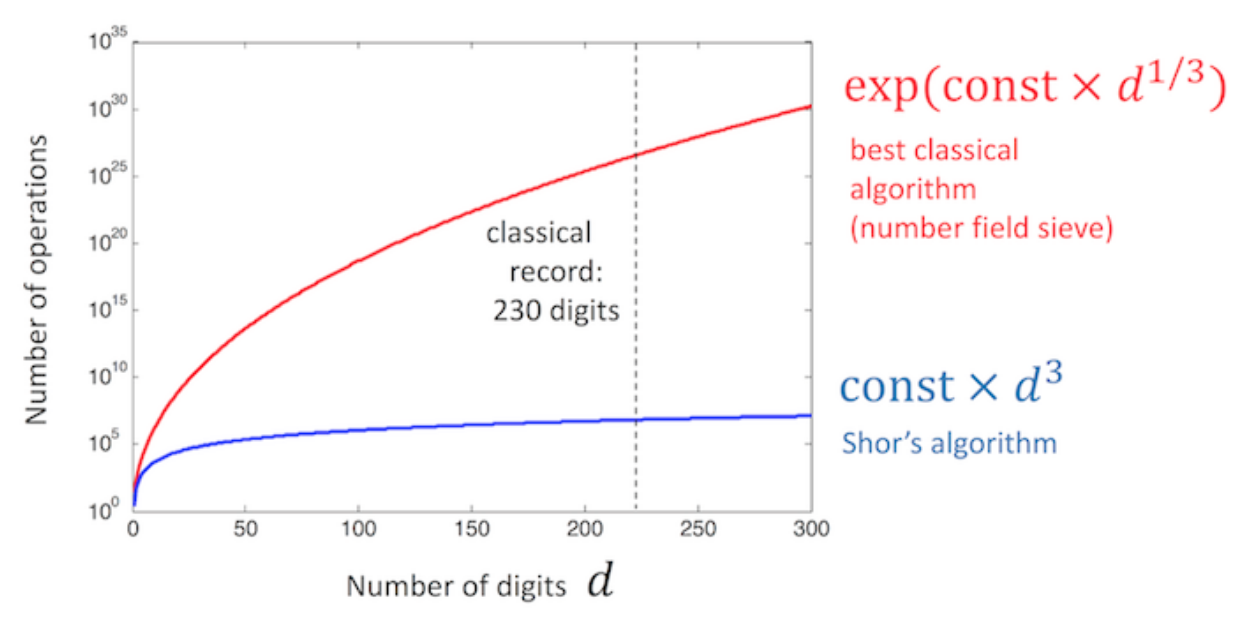
离散对数的问题是通过y = g^x mod p来寻找x,利用Shor算法快速找到周期,从而进行求解。
设函数
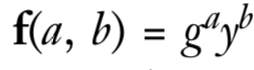
要找到周期ω和ω‘,满足
f(a+w,b+w')=f(a,b)
通过上式可以推出
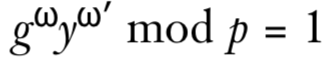
使用g^x代替y,可以得到
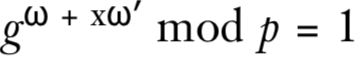
这等价于
![]()
所以可以得出x=-w/w'
算法复杂度为O(n^2(log n)(log log n)),其中n是p的比特长度
除了Shor算法之外,另一个经典的量子加速就是以√n复杂度搜索n个元素的能力(在经典算法中,其复杂度为O(n)),这种加速可以通过Grover算法实现,于1996年由计算机科学家洛夫·格罗弗提出,Grover算法的量子电路表示如下。
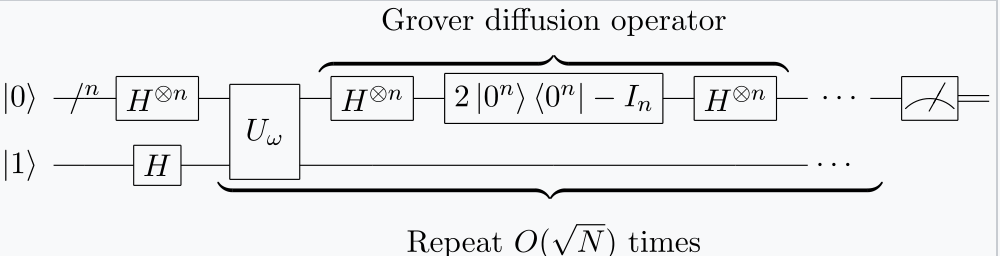
简单起见,我们可以把Grover算法当做从n个可能的值中找到满足f(x)=1中的x的一种方法,其中f满足:f输出为0或1,对于大部分输入都会输出0。如果有m个x值满足f(x)=1,那么Grover算法可以在O(√n/m)时间内找到解
把f放到密码学的场景下,设f(x)=1当且仅当x等于加密函数E(K,P)=C的未知密钥K。如果E是AES的话,找x相当于就是找到密钥,如果使用Grover算法,那么时间复杂度为2^64量级,
而使用经典计算机则是2^128量级。
此外,Grover算法还可以用于哈希函数的原像攻击,其通过2^(n/2)量级运算就可以找到n比特哈希函数的原像。
有关的具体理论分析可以阅读原始论文《A fast quantum mechanical algorithm for database search》。
后量子密码是指不会被量子计算机攻破的密码,这也就意味着这些算法不能依赖于会被Shor算法等解决的难题。目前主要的类型有四种:基于编码的,基于格的,基于多变量的,基于哈希的。在NIST PQC比赛第三轮决赛时的算法按照类别分组可以表示如下。
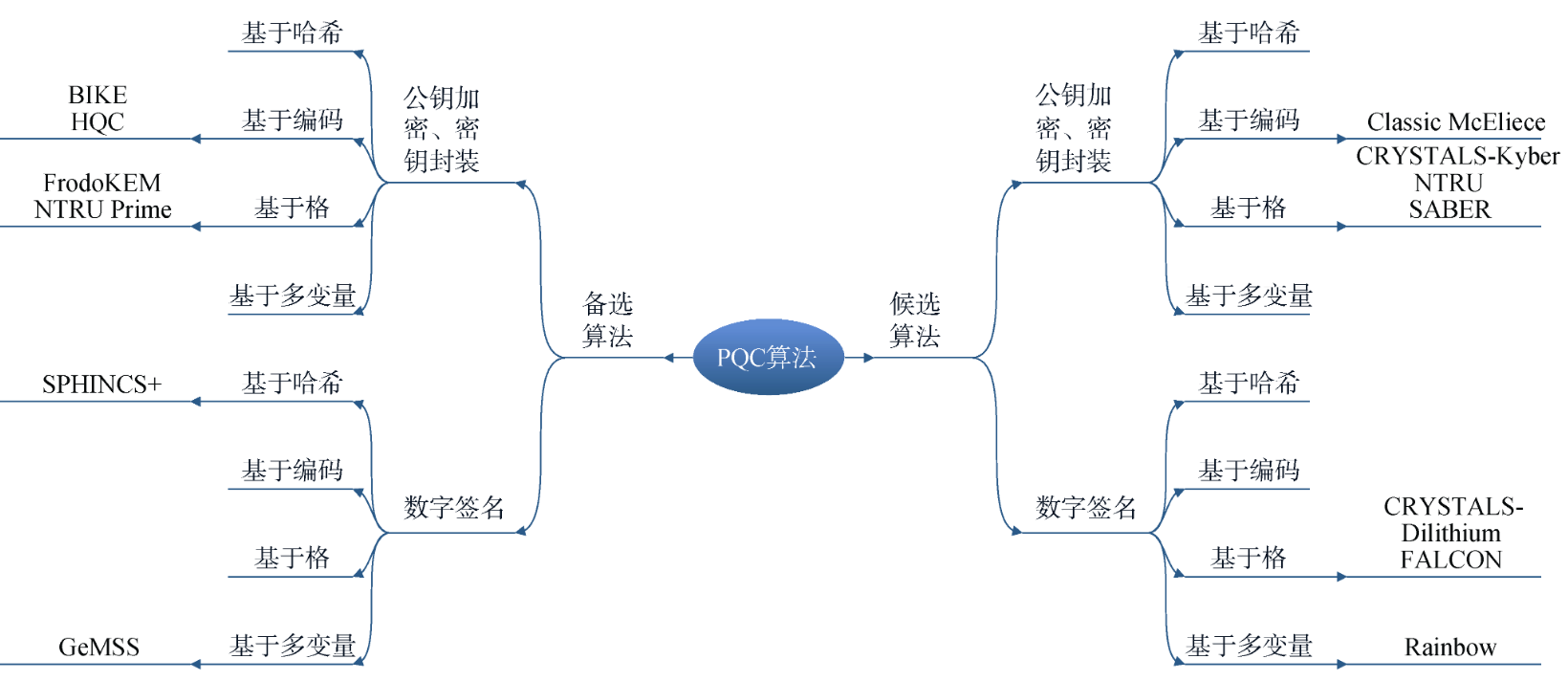
基于哈希的签名方案的安全性来源于Hash函数的安全性, 典型方案为默克尔(Merkle)签名方案, 由一次性签名方案OTS (One Time Signature)演变而来的, 并结合了Merkle的哈希树认证机制, 共同构造出一个完全的二叉树来实现数字签名。哈希树的根是公钥, 一次性的认证私钥是树中的叶子节点。
基于编码理论构造的公钥体制, 其理论基础是解码问题的困难性, 换句话说就是在已知生成矩阵的情况下, 在码空间寻找一个码字与已知码的Hamming距离最短。如果已知码为0则问题就是最小权重问题。它的任意线性码的译码问题是NP完全问题。
基于格的公钥密码体制是在大维数的格上, 基于最短向量问题SVP (Shortest Vector Problem)和最近向量问题CVP (Closest Vector Problem)等数学难题而构造的公钥密码体制。SVP问题是指在大维数格中寻找长度最短的非零向量, 而CVP是指在大维数格中寻找和固定向量距离最近的向量, 这两个问题都是NP难问题。
基于多变量的算法使用有限域上具有多个变量的二次多项式组构造加密、签名、密钥交换等算法。它的安全性来源于求解有限域上随机生成的多变量非线性多项式方程组。该问题被证明为非确定性多项式时间困难。目前没有已知的经典和量子算法可以快速求解有限域上的多变量方程组。
它们横向的比较分析可以总结如下
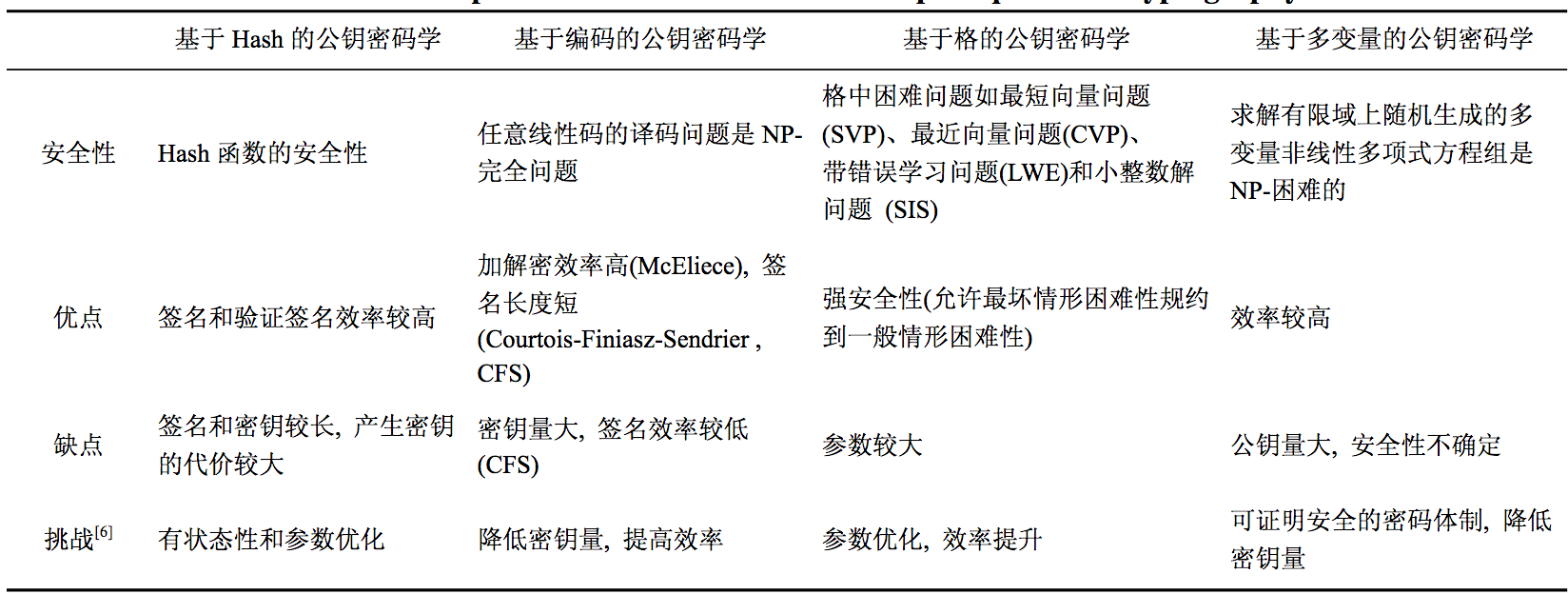
如果对后量子密码学有兴趣,可以进一步参考《The Survey of Post-quantum Cryptography Hardware Implementation 》等文献。
1.https://qrunes-tutorial.readthedocs.io/en/latest/chapters/algorithms/shor_Algorithm.html
2.https://en.wikipedia.org/wiki/Shor%27s_algorithm
3.https://web.archive.org/web/20190702011957/https://seclists.org/fulldisclosure/2019/Jun/46
4.https://csrc.nist.gov/Projects/elliptic-curve-cryptography
5.https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2016-0701
6.https://en.wikipedia.org/wiki/Computational_Diffie%E2%80%93Hellman_assumption
7.https://en.wikipedia.org/wiki/Decisional_Diffie%E2%80%93Hellman_assumption
https://zhuanlan.zhihu.com/p/255171562
9.《Handbook of Elliptic and Hyperelliptic Curve Cryptography》
10.《Quantum Computing and Quantum Information》
11.https://arxiv.org/abs/quant-ph/9605043
12.https://docs.microsoft.com/zh-cn/azure/quantum/concepts-grovers
13.《Serious Cryptography》
14.The Survey of Post-quantum Cryptography Hardware Implementation
15.《Elliptic Curve Cryptography in Practice》
16.https://link.springer.com/chapter/10.1007/978-3-319-24174-6_21