-
在线客服
QQ扫码联系在线客服
QQ: 2292620539
-
在CTF杂项题型中,盲水印的出现频率是相当高的,但大多数人处于只会用脚本的阶段,没有对原理进行深入理解,这篇文章主要把盲水印的原理和解题过程总结一下。
盲水印的基本原理如图所示:
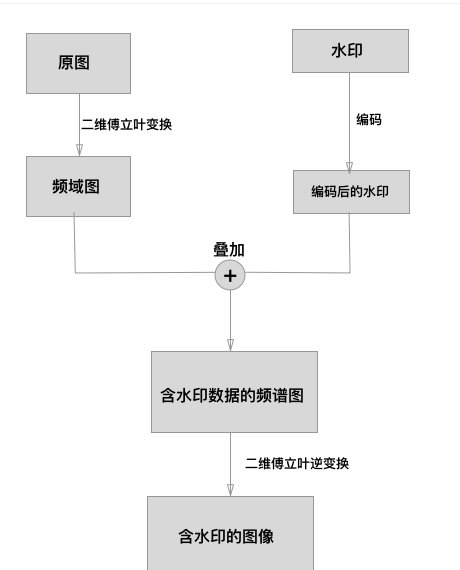
主要的知识点在于傅里叶变换把原图变为频谱图,再叠加水印,将含水印的频谱图进行傅里叶逆变换得到含水印的图像。那么思考傅里叶变换如何将原图变为频谱图,再将频谱图变为图像呢?下面对傅里叶变换进行分析。
傅里叶变换涉及的知识点太多了,第一次接触傅里叶分析的读者可以先参考一下这篇文章,傅里叶分析之掐死教程(完整版)。下面介绍一下傅里叶变换的一些前置知识。
介绍一下频域,时域。以音乐为来举例子,时域就是我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。以音乐为例,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
时域的基本单元就是“1秒”,如果我们将一个角频率为$\omega_0$的正弦波$cos(\omega_0)$看作基础,那么频域的基本单元就是有了“1”,频域的“0”就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状,鉴于正弦波是周期的,我们需要设定一个用来标记正弦波位置的东西。也就是相位。
最后借用文章的一张图:
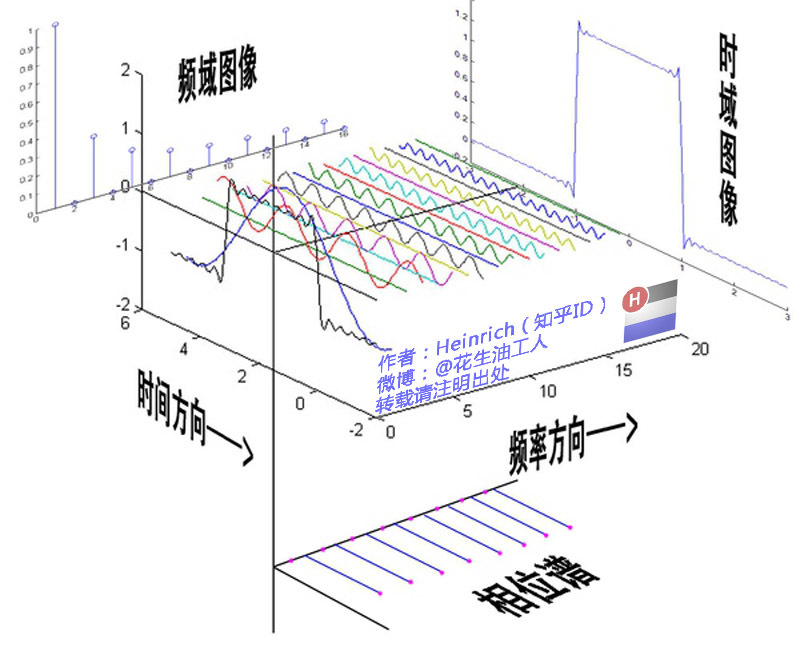
傅里叶的原理表明,任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。利用傅立叶变换算法直接测量原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位就可以表示原始信号。其等价关系可以表示为:
$$
f(原始信号)=A_1sin(\omega_1x+\phi_1)+A_2sin(\omega_2x+\phi_2)+...
$$
再来看看图像的傅里叶变换,上述举得例子是一维信号的傅里叶变换,并且信号是连续的,我们知道图像是二维离散的,连续与离散都可以用傅里叶进行变换,那么二维信号就是在$x$方向与$y$方向都进行一次一维的傅里叶变换得到。下面看看二维傅里叶变换,一个图像为$M*N$的图像$f(x,y)$进过离散傅里叶变换得到$F(u,v)$,那么一般的公式为:
$$
F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(ux/M+vy/N)}
$$
它的反变换就是
$$
F(x,y)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(u,v)e^{j2\pi(ux/M+vy/N)}
$$
反变换就可以实现将频域图像恢复到时域图像。对正变换分析,当u=v=0时,那么:
$$
F(0,0)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)
$$
这个式子f(x,y)就是时域里面图像的灰度。其实是整个图像的灰度求平均。在计算机领域中,灰度数字图像是每个像素只有一个采样颜色的图像。这类图像通常显示为从最暗黑色到最亮的白色的灰度,尽管理论上这个采样可以任何颜色的不同深浅,甚至可以是不同亮度上的不同颜色。灰度图像与黑白图像不同,在计算机图像领域中黑白图像只有黑白两种颜色,灰度图像在黑色与白色之间还有许多级的颜色深度。那么F(0,0)在频域内称为直流分量,其他的所有F称为交流分量,直流分量可以看到是在0处获得的,所以很明显是存在于低频分量下的。为了便于观察,我们常常使直流成分出现在窗口的中央,可采取换位方法,变换后中心为低频,向外是高频。
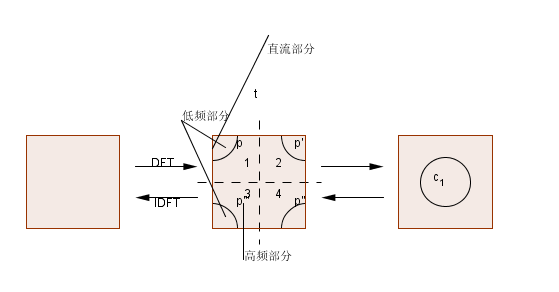
在分析图像信号的频率特性时,对于一幅图像,直流分量表示预想的平均灰度,低频分量代表了大面积背景区域和缓慢变化部分,高频部分代表了它的边缘,细节,跳跃部分以及颗粒噪声等。
对于水印和原图,我们很容易得到时域表示$f1,f2$ ,为了让水印的信息能在频域上尽量平均分布,引入随机变换$r(f)$ 来对时域上的水印进行变换,即
$$
f\prime_2=r(f_2)
$$
同时我们对原图进行二维离散傅里叶变换
$$
F_1=FFT2(f_1)
$$
接下来我们引入能量系数 对水印和原图频域合成得到
$$
F=F_1+\alpha f\prime_2
$$
然后逆变换我们就得到了加了盲水印的图片(时域表示)
$$
f=IFFT2(F)
$$
如果想解水印,那么首先对$f$ 变换得到$F$
$$
F=FFT2(f)
$$
然后减去原图的频域并且做随机变换$r$ 的逆变换就得到了水印的时域表示
$$
f_2=r^{-1}(\frac{F-F_1}{\alpha})
$$
这就是图片盲水印的基本原理。
因为 $F(u,v)$ 和$F(-u,-v)$ 是共轭的,的它们的实部应该是一样的,如果实部不一样的话逆变换回去势必在虚部上会损失一部分信息(我们写入图片的时候只用实部),考虑到我们想尽量提高盲水印的隐匿性,所以我们的水印应该是关于图片中心对称的。
由于在频域叠加的时候我们一般的策略是让水印信息尽可能随机分布在原图频域的所有分信号上,因此在逆变换回时域后整体图片其实差别并不大。
在前面推导盲水印的过程中,我们实际上有一个密匙 $k={{\alpha,r}}$ ,因为只有知道了$k$和原图,才能完成解水印的过程, 这相当于完成了简单的对称式加密,也就是说即使攻击者知道图片加了盲水印,由于没有 $k$(和原图),也无法去掉盲水印或者替换盲水印。
有时候攻击者可能对图片进行处理比如剪裁、压缩等,由于盲水印已经将信息分布在了频域的各个分信号上,因此可以有效抵抗这些攻击。
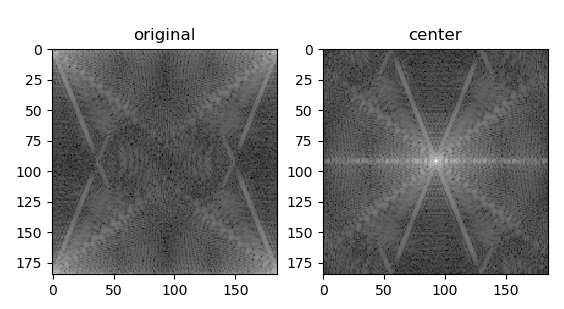
现在我们用蚁景网安的图标来演示:

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('hetian.jpg',0) #直接读为灰度图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)#将图像中的低频部分移动到图像的中心
#取绝对值:将复数变化成实数
#取对数的目的为了将数据变化到较小的范围(比如0-255)
s1 = np.log(np.abs(f))
s2 = np.log(np.abs(fshift))
plt.subplot(121),plt.imshow(s1,'gray'),plt.title('original')
plt.subplot(122),plt.imshow(s2,'gray'),plt.title('center')
plt.show()运行结果如下所示:
频域变换到时域的操作就是逆向傅里叶变换再走一遍(比如先反中心化,在逆变换)。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('hetian.jpg',0) #直接读为灰度图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
#取绝对值:将复数变化成实数
#取对数的目的为了将数据变化到0-255
s1 = np.log(np.abs(fshift))
plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')
plt.subplot(132),plt.imshow(s1,'gray'),plt.title('center')
# 逆变换
f1shift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f1shift)
#出来的是复数,无法显示,取绝对值
img_back = np.abs(img_back)
plt.subplot(133),plt.imshow(img_back,'gray'),plt.title('img back')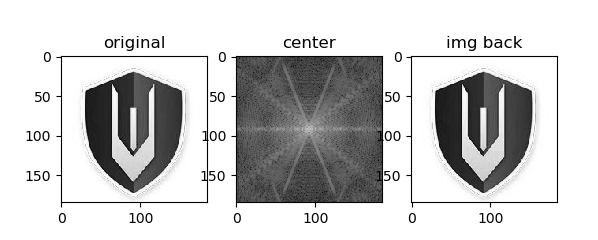
到这里我们已经理解完盲水印的基本原理了,下面我们开始实践。在CTF比赛中,遇到盲水印的题目我会使用github上的盲水印脚本。我们利用该脚本进行盲水印加密和解密。
我们在当前目录下有三个文件,分别为脚本文件,原图(hetian.png)和水印(flag.png)。

运行完生成hetin2.png和flag2.png。
其中flag2.png可以很清楚的看到水印。

接下来我们对盲水印的隐匿性进行探究,首先我们对hetian2.png加上合天的文字,如图所示:

然后进行盲水印解密

可以看到解出来处理的水印变得模糊,但还是可以清楚地看出水印的内容,说明盲水印鲁棒性比较好。